그래픽 라이브러리를 사용하지 않는 이유
3차원 그래픽 사용 시
- 게임 엔진
- 언리얼 엔진
- 유니티 엔진
- 그래픽 라이브러리
- DirectX
- OpenGL
점 찍는 기능에서 출발해서 모든 것을 직접 구현해 보자.
→ 3차원 그래픽과 관련된 연산 과정을 그래픽 카드에 일임한다. 따라서 렌더링 파이프라인에서 사용되는 핵심적인 수학을 알 길이 없다.
가장 확실한 공부 방법은 밑바닥에서부터 하나씩 만들어 나가는 것.
공리에서부터 시작하여 하나씩 쌓아 나가기.
게임 수학의 분류
- 공간에 대한 수학
- 물체에 대한 수학
- 회전에 대한 수학
공간에 대한 수학
게임 세계 == 현실 세계를 모방한 가상 세계
현실 세계와 게임 세계가 움직이는 원리는 완전 다르다고 생각해야 한다.
컴퓨터로 구성된 세계는 '수'를 통해 쌓아 올려진 명확한 시스템 ⇒ 벡터 공간(Vector Space)
벡터 공간(Vector Space): 게임이 사용하는 가상 공간의 본질. 수의 체계에 의해서 쌓아 올린 다차원의 데이터라고 생각하자.
물리학의 벡터와 스칼라
벡터: 크기와 방향을 가진 대상
스칼라: 크기만 있는 물리량
수학에서의 벡타와 스칼라
벡터: 벡터 공간의 원소
스칼라: 체 집합의 원소
'수'와 '연산'이 만들어내는 시스템이라고 이해하자.
가장 밑바닥의 원리를 이해하는 것이 가장 중요하다.
변환(Transformation)
1초에 60 프레임을 찍어내야 하는 게임의 특성상, 변환이 빠르고 단순하고 명료하게 이루어져야 한다.
⇒ 선형 변환 (Linear Transformation)
선형 변환을 통해 빠르게 공간을 변환하고, 변환된 공간도 원래대로 돌리는 게 가능해진다.
현실 세계의 공간은 하나뿐이지만, 수가 만들어내는 공간(게임 공간)은 수의 개수만큼 무한하다.
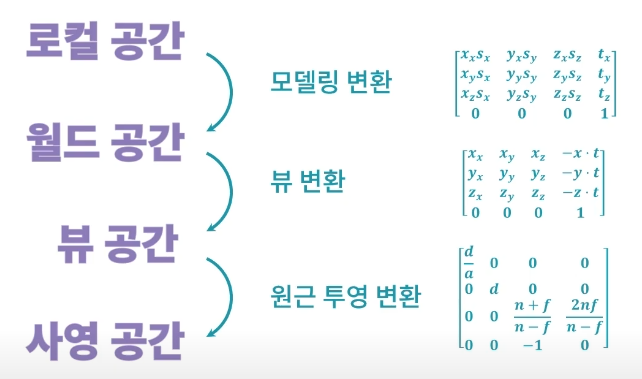
렌더링 파이프라인
컴퓨터에게 일을 지시하기 위한 게 행렬(Matrix)이다.

공간 변환을 실제로 구현해 보기 위해서는 주어진 행렬을 암기하는 게 아닌, 행렬이 어떻게 만들어지는지, 어떻게 설계해야 하는지 '기본 원리'를 이해하는 게 가장 중요하다.
메커니즘을 이해한 후, 평면의 방정식(ax + by + cz + d = 0)을 이해한다. 이를 통해 영역을 구축할 수 있으며, 구축된 영역 안에서 어떠한 작업을 할지 수학을 사용하여 지정할 수 있다.
ex) 카메라가 보는 절두체(Frustum). 보이는 물체만 렌더링하는 수학적인 메커니즘이 만들어지게 되며, 1초에 60프레임 렌더링이 가능하게끔 한다.
중요한 것
수의 체계와 벡터 공간 - 벡터, 수의 체계 등의 탄탄한 이해
선형 변환과 행렬 - 수를 통해서 변환하는 그 과정
해당 포스트는 이득우 교수님의 '수포자를 위한 게임 수학' 동영상을 보며 개인 백업용으로 메모하였습니다.
