학습개요
- 수학은 인류의 역사와 함께 시작된 학문이며, 당면한 현실 문제를 추상화 또는 일반화하여 문제를 논리적으로 해결할 수 있도록 한다.
- 수학은 무엇이며 왜 수학을 배우는지를 정리하고, 수학논리와 수의 체계 등 대학수학의 기초가 되는 내용을 살펴본다.
- 수의 체계에서는 실수 중심으로 여러 가지 성질을 살펴본다.
학습목표
- 수학의 정의를 이해할 수 있다.
- 수학의 기초 논리를 이해할 수 있다.
- 수의 체계를 이해할 수 있다.
정리하기
- 수학은 현실 문제를 추상화 또는 일반화하여 그 문제를 논리적으로 해결할 수 있는 학문이다.
- 수학의 명제는 연역법, 귀류법, 수학적 귀납법으로 증명한다.
- 실수는 유리수와 무리수로 구성되어 있다. 두 실수가 있다면 대소의 순서가 있고, 덧셈과 곱셈에 대해 교환법칙, 결합법칙, 분배법칙이 성립하며 항등원과 역원이 존재한다.
- 두 실수 사이의 모든 점의 모임을 구간이라고 한다.
학습내용
수학의 정의
수학이란
- 수학 : 원리들을 보기 어렵기 때문에 자연 및 사회현상을 추상화, 일반화하여 문제를 논리적으로 해결할 수 있는 기본 원리를 제공.
- 학문에 필요한 논리를 제공하는 과학의 언어.
- 현대 과학.
- 자연 과학 ⇒ 물리학, 천문학...
- 사회 과학 ⇒ 경제학, 경영학, 사회학...
- 공학
수학의 역사
- 농경생활 할 때도 측정, 관찰하던 도구로 수학을 사용.
- 그리스부터 플라톤, 유클리드 등 본격적으로 연구되었다.
- 17세기 미적분학 등 해석학 발전. 뉴턴, 라이프니츠, 오일러, 데카르트, 파스칼 등...
- 과학 혁명이 오기 전, 수학에서 많은 발전들이 이루어졌다. 그 이후로는 굉장히 추상적으로 발전이 되었다.
- 순수수학 : 수학 그 자체를 연구
- 응용수학 : 순수수학에서 얻어진 이론을 바탕으로 현실 문제를 구체화
- 오일러(L. Euler)
- 18세기 인물. 논문을 500편이나 썼다...! 러시아, 독일.
- 미적분학 발전
- 기호 정리 (f(x), sin, cos, pi...)
- 쾨니히스베르크의 다리 문제 → 한붓 그리기 (추상화) → 그래프 이론, 네트워크 이론으로 발전.
- 에라토스테네스
- 그리스의 학자.
- 위도, 경도
- 에라토스테네스의 지구둘레 측정
- 수학은 광의적, 협의적 정의 가능
- 복잡한 현실의 문제를 단순하게 추상화한 후, 이를 수학적 원리로 해결하고 결과를 현실에 적용하는 학문.
수학의 기초 논리
- 수학: 추상화된 문제를 정리 등을 통해 해결
정리
- 정리: 가정 → 결론 (P → Q)라는 "명제"
- 정리의 증명: P가 사실이면 Q가 사실임을 보임 (대우명제 ~Q → ~P)
- P → Q가 참이면, P는 Q가 되기 위한 충분조건, Q는 P가 되기 위한 필요조건
- P ↔ Q: 필요충분조건
명제의 증명
- 연역법: 몇 개의 명제가 옳다고 가정한 후, 다른 명제가 옳다는 것을 논리적으로 밝히는 방법
- 귀류법: 직접 증명하기 어려울 때, 명제의 결론을 부정하고 "모순"을 보이는 증명 방법
- 수학적 귀납법: 자연수에 대한 명제가 모든 자연수에 대해 성립함을 보이는 증명 방법
정수 $n$이 짝수이면 $n^2$는 짝수이다.
$n = 2k$ (k는 정수)
$n^2 = (2k)^2 = 4k^2 = 2*(2k^2)$
따라서 $n^2$는 짝수.
역도 성립. ($n^2$이 짝수이면 $n$도 짝수이다.)
$\sqrt{2}$는 무리수임을 증명하시오.
실수 → 유리수(순환소수로 표현되지 않는 수, $a \over b$), 무리수
$\sqrt{2} = \frac{a}{b}$ ($a, b$는 서로 소임, $b \neq 0$, $\sqrt{2}$는 유리수라고 가정)
$2 = {a^2 \over b^2}$, $a^2 = 2b^2$
$a^2$은 짝수, $a$는 짝수
$a = 2k$, $k$는 정수
$4k^2 = 2b^2, b^2 = 2k^2$
따라서 $b^2$는 짝수, $b$는 짝수
$a, b$ 모두 짝수
⇒ 서로소라는 가정에 위배
⇒ 유리수 X
따라서 $\sqrt{2}$는 무리수!
자연수 $n$에 대하여 $1 + 2 + ... + n = \frac{n(n+1)}{2}$임을 보이시오.
$n = 1$일 때, $1 = \frac{1(1+1)}{2} = 1$ 성립
$n = k$일 때, $1 + 2 + \cdots + k = \frac{k(k+1)}{2}$가 성립한다고 가정한다.
$n = k + 1$, $1 + 2 + \cdots + k + k + 1 = \frac{k(k+1)}{2} + (k+1)$
$\frac{k(k+1)}{2}+(k+1) = \frac{1}{2}k^2 + \frac{1}{2}k+k+1$
$= \frac{1}{2}(k^2 + 3k+2)$
$=\frac{1}{2}(k+1)(k+2)$
$n=k$ 성립 ⇒ $n = k + 1$ 성립
$\therefore$ 모든 자연수에 대해서 $1+2+\cdots+n=\frac{n(n+1)}{2}$ 성립.
수의 체계와 성질
- 대학수학은 실수체계를 바탕으로 설명한다.
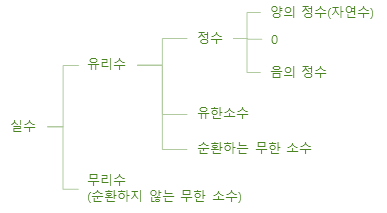
실수

- 실수
- 유리수: $\frac{a}{b}$로 딱 떨어진다. $a, b$는 서로소.
- 정수
- 자연수: 숫자를 세기 위해서. 1, 2, 3, 4...
- 0과 음수: 0, -1, -2, -3, -4...
- 정수가 아닌 유리수
- 유한소수: 딱 떨어지는 유리수. 0.5, 0.125
- 순환소수: 0.333..., 0.166...
- 무리수 (순환하지 않는 무한소수): $\sqrt{2}, \sqrt{3}, \pi, e$
- 정수
- 유리수: $\frac{a}{b}$로 딱 떨어진다. $a, b$는 서로소.
- 실수의 성질
- 실수: 유리수 + 무리수
- 실직선, 실수가 일대일 대응된다.
- $a$가 실수라면 $a>0$ 또는 $a = 0$ 또는 $a < 0$
- 교환법칙: $a+b=b+a,\ ab=ba$
- 결합법칙: $(a+b)+c=a+(b+c),\ (ab)c=a(bc)$
- 분배법칙: $a(b+c)=ab+ac$
- 항등원: $a+0=a,\ a*1=a$
- 역원: $a+(-a)=0, \ a*a^{-1}=1$
- 실수의 크기 비교
- $a > b,\ b>c\ \Rightarrow\ a>c$
- $a>b\ \Rightarrow\ a+c>b+c,\ a-c>b-c$
- $a>b,\ c>0\ \Rightarrow\ ac>bc,\ {a \over c}>{b \over c}$
- $a>b,\ c<0\ \Rightarrow\ ac<bc,\ {a \over c}<{b \over c}$
절댓값
- $\left\vert a \right\vert,\ a \geq 0$
$\left\vert a \right\vert = -a,\ a < 0$ - $\left\vert a \right\vert \ge 0,\ |a|=|-a|$
- $|ab|=|a||b|$
- $|{a \over b}|={|a| \over |b|}$
$|a+1|+|a-2|$를 $a$의 범위에 따라 정리하시오.
- $a\ge2 \Rightarrow a+1\ge0,\ a-2\ge0$
$(a+1)+(a-2)=2a-1$ - $-1 \le a < 2 \Rightarrow a+1\ge0,\ a-2 < 0$
$(a+1)-(a-2)=3$ - $a<-1\Rightarrow a+1<0,\ a-2<0$
$-(a+1)-(a-2)=-2a+1$
구간
- 구간 : 두 실수 사이의 모든 점의 모임
- 구간의 표현
- $\{x|a<x<b\} \rightarrow$ ($a, b$)
- $\{x|a \le x \le b\} \Rightarrow$ [$a, b$]
- $\{x|a \le x<b\} \Rightarrow$ [$a, b$)
- $\{x|a<x\} \Rightarrow$ ($a, +\infty$)
- $\{x|x \le b\} \Rightarrow$ ($-\infty, b$]
- 폐구간 [포함]
- 개구간 (포함 안 함)
실수 직선의 특징
- 실수 직선 $R$은 $(-\infty, +\infty)$로 표현
- 실수는 조밀(dense)하다.
- 조밀하다: 실수 $a$와 $b$ 사이에 수많은 숫자가 존재한다. 가득 차 있다.
구간의 상계와 하계
- b보다 크거나 같은 실수 ⇒ 상계
- a보다 작거나 같은 실수 ⇒ 하계
- $S = \{x|a \le x \le b\}$
- $S = \{x|a \le x \}$
$S_1 = [5, \infty),\ S_2=[0,2)$
- $S_1$ - 하계: 5보다 작거나 같은 실수, 상계는 없음, 최솟값: 5, 최대값 없음
- $S_2$ - 하계: 0보다 작거나 같은 실수, 상계는 2보다 큰 수, 최솟값 2, 최대값은 없음
최소상계와 최대하계
- 최소 상계 : 모든 상계 중 최소인 수, sup S
- 최대 하계 : 모든 하계 중 최대인 수, inf S
- $S_1 = [0, 5]$ 최소 상계: 5
해당 포스트는 방송통신대학교의 '대학수학의 이해' 강의를 들으며 개인 공부 목적으로 메모하였습니다.
