Published 2021. 9. 20. 19:07

선형대수 - 1. 일차연립방정식

방송대/선형대수

학습개요

일차연립방정식에 관하여 학습한다.
기본적인 일차방정식의 풀이 방법을 공부한다.
유일한 해를 갖는 경우, 무수히 많은 해를 갖는 경우(부정), 해를 갖지 못하는 경우(불능) 등 세 가지 경우가 있다는 점에 유의한다.
n원 일차연립방정식이 무엇인지 배우고, 이것을 풀기 위해 사용되는 소거법에 관해 학습한다. 소거법은 '방정식에 관한 3가지 기본 연산'을 이용한다.
2원 일차연립방정식을 예로 들어, 유일한 해를 갖는 경우, 불능의 경우, 부정인 경우 각각에 대해 그래프를 이용하여 기하학적인 의미를 확인한다.
일차연립방정식의 활용 예제를 배운다.

학습목표

간단한 일차방정식 $ax = b$가 어떤 경우에 유일한 해를 갖는지, 불능이 되는지, 부정이 되는지를 설명할 수 있다.
일차연립방정식에서 사용되는 기본 용어(계수, 미지수, 상수, 해, 부정, 불능 등)에 대해 설명할 수 있다.
'방정식에 관한 3가지 기본 연산'이 무엇인지 설명할 수 있다.
간단한 1원 일차연립방정식을 풀 수 있고, 해당 방정식을 2차원 평면에 그래프로 그려 기하학적인 의미를 설명할 수 있다.

들어가기

맛보기 문제 (1) : 비행기 속도

서울에서 500km 떨어져 있는 곳(타슈켄트). 서울에서 갈 때는 6.5시간, 서울로 올 때는 5.0시간?

바람까지 포함한 속력을 생각해 본다.

x : 비행기 속도 - 음수가 될 수 없고
y : 바람 속도 - 비행기와 같은 방향으로 불 때는 양수, 다른 방향으로 불 때는 음수
⇒ 일차연립방정식

$\begin{cases} 6.25(x-y) = 5000 \\ \quad\ 5(x+y) = 5000 \end{cases}$

$\begin{cases} x-y = 800 \\ x+y = 1000 \end{cases}$

두 식을 더하면 $2x = 1800$ $\therefore x = 900km/h$, $y = x - 800 = 900 - 800 = 100 km/h$

맛보기 문제 (2) : regression (회귀 분석)

Machine Learning에서 선형대수
Polynomial(다항식) Curve Fitting

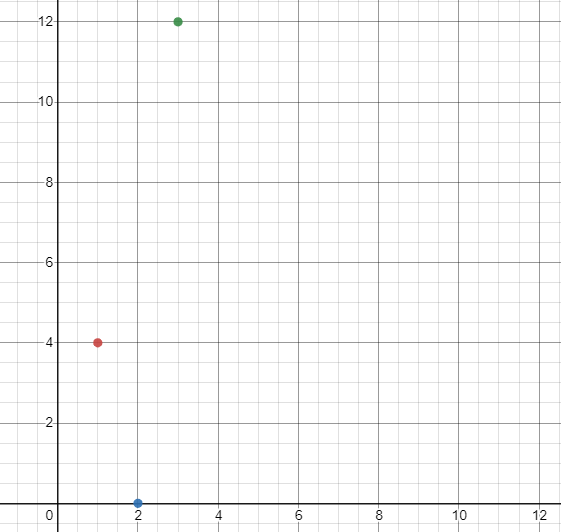
평면에서 세 점 $(1, 4), (2, 0), (3, 12)$을 지나는 2차 곡선을 구하시오.

$y = ax^2 + bx + c$

$a + b + c = 4$ (1, 4를 대입)

세 점을 찍었을 때, 1차 직선으로 Curve Fitting하는 건 어려울 듯하다. ⇒ 2차 곡선으로!

2차 곡선 : $p(x) = a_0 + a_1x + a_2x^2$

$\begin{cases} p(1) = a_0 + a_1 + a_2 = 4 \\ p(2) = a_0 + 2a_1 + 4a_2 = 0 \\ p(3) = a_0 + 3a_1 + 9a_2 = 12 \end{cases}$

⇒ $a_0, a_1, a_2$가 미지수인 일차연립방정식을 풀면 된다.

$a_0 = 24, a_1 = -28, a_2 = 8$

$p(x) = 24 - 28x + 8x^2$

학습목표

다음을 설명할 수 있다.

일차방정식 ax = b의 해법
n원 일차연립방정식
일차연립방정식의 계수, 상수, 미지수, 해
소거법
방정식에 관한 3가지 기본 연산
일차연립방정식 해의 기하학적 의미
일차연립방정식의 응용 사례

학습내용

일차연립방정식

$ax = b$
$\begin{cases} x+y = 3 \\ x-y = 1 \end{cases}$
두 식을 빼면... $2y = 2$ ⇒ $ax = b$

$ax = b$ ⇒ $x = {{b}\over{a}}$ , $x = a^{-1}b$

$ax = b$
- a : 계수(coefficient)
- x : 미지수(unknown)
- b : 상수(constant)
- 이 방정식에 맞는 x : 해 (solution) = 근

$x = {b \over a}$ ⇒ 만약 $a$가 0이라면?
좋은 프로그래머는 사실 초년생 프로그래머와 다를 게 없다. 문제 해결할 때는 99% 비슷하나, 예외 처리 능력이 있느냐 없느냐가 고급 프로그래머의 경험으로부터 나온다. 좋은 프로그래머가 되기 위해서는 경우의 수를 잘 생각해 봐야 한다.

$a \neq 0$인 경우
- $a^{-1}$ 가 존재 ⇒ $a^{-1}ax = a^{-1}b$ ⇒ $x = a^{-1}b$ (유일한 해)
$a = 0$인 경우, $ax$는 무조건 0이 된다 ⇒ 두 가지 경우! $b = 0, b \ne 0$
$a = 0, b = 0$인 경우
- $0x = 0$ ⇒ 무수히 많은 해, 부정(不定)
$a =0, b \ne0$인 경우
- $0x =b$ ⇒ 해가 없음, 불능(不能)

n원 일차연립방정식

n원일차연립방정식: 미지수가 n개인 일차방정식들을 유한개 묶어 놓은 것
- $\begin{cases} a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n = b_m \\ \end{cases}$
n원 일차연립방정식의 해(근)
- $\begin{cases} a_{11}S_1 + a_{12}S_2 + ... + a_{1n}S_n = b_1 \\ a_{21}S_1 + a_{22}S_2 + ... + a_{2n}S_n = b_2 \\ \vdots \\ a_{m1}S_1 + a_{m2}S_2 + ... + a_{mn}S_n = b_m \\ \end{cases}$
- 이를 만족시키는 순서조 $(S_1, S_2, ..., S_n)$를 해[근]라고 한다.
- 순서쌍은 두 개일 때 부르는 용어.

예제 1.1 3원 일차연립방정식의 해

2차 곡선: $p(x) = a_0 + a_1x + a_2x^2$

$\begin{matrix} p(1) = a_0 + a_1(1) + a_2(1)^2 = a_0 + \ \ a_1+ \ \ a_2 = 4 \\ p(2) = a_0 + a_1(2) + a_2(2)^2 = a_0 + 2a_1+ 4a_2 = 0 \\ p(3) = a_0 + a_1(3) + a_2(3)^2 = a_0 + 3a_1+ 9a_2 = 12 \end{matrix}$

$a_1 \rightarrow x, a_2 \rightarrow y, a_3 \rightarrow z$

$\begin{cases} x+\ \ y+\ \ z = 5 \\ x+2y+4z = 0 \\ x+3y+9z = 12 \end{cases}$

소거법

다음의 3가지 연산을 이용하여 주어진 연립방정식을 동일한 해집합을 가지면서 보다 풀기 쉬운 형태의 연립방정식으로 변환하는 방법

두 방정식을 교환한다.
한 방정식에 0이 아닌 상수를 곱한다.
한 방정식에 임의의 상수를 곱하여 다른 방정식에 더한다.

⇒ 방정식에 관한 3가지 기본 연산

예제 1.2 다음을 소거법으로 풀어라.

$\begin{matrix} 2x-y&=&-1\\x + y &=& 4 \end{matrix}$

(1) 두 방정식을 교환한다.

$\begin{matrix} x+y&=&4\\2x-y&=&-1 \end{matrix}$

(3) 임의의 상수를 곱하여 다른 방정식에 더한다.

$\begin{matrix} -2x-2y&=&-8\\2x-y&=&-1 \end{matrix}$

두 식을 더하면 $-3y = -9$, $\therefore y=3, x=1$

정답 - 순서쌍 (1, 3) : 해

또는, 처음 식에서 $y$의 계수가 부호만 다르기 때문에 두 식을 더해 줘도 된다.

$\begin{matrix} 2x-y&=&-1\\x + y &=& 4\\\\3x&=&3 \end{matrix}$

$\therefore x=1$

기하학적 설명

$\begin{matrix} y=2x+1\\y=-x+4 \end{matrix}$

예제 1.3

$\begin{matrix} 2x+2y&=&8\\x+y&=&2 \end{matrix}$

$\begin{matrix} y=-x+4\\y=-x+2 \end{matrix}$

교점이 없음 → 해를 구하지 못함 (불능)

예제 1.4

$\begin{matrix} 2x+2y&=&8\\x+y&=&4 \end{matrix}$

$\begin{matrix} y=-x+4\\y=-x+4 \end{matrix}$

방정식이 두 개인 줄 알았더니 같은 방정식이었다! → 교점이 무수히 많음 (부정)

일차연립방정식의 응용

화학반응식
유리함수의 부분 분수로 나누기
교차로에서의 자동차 흐름
Curve fitting
Linear programming
Network analysis
- Car traffic analysis
- Electrical network analysis